Корреляционный анализ в Excel: пошаговое руководство

Microsoft Excel предоставляет широкие возможности для статистического анализа, включая инструменты для проведения корреляционного анализа. Корреляционный анализ помогает выявить и количественно оценить взаимосвязь между различными переменными, что имеет критическое значение при принятии решений на основе данных. 

Определение степени и характера взаимосвязи между показателями позволяет точнее прогнозировать результаты, выявлять скрытые зависимости и оптимизировать бизнес-процессы. Excel делает этот статистический метод доступным для всех пользователей благодаря встроенным функциям и инструментам, не требующим глубоких знаний в области программирования или статистики.

Что такое корреляционный анализ

Корреляционный анализ – это статистический метод, который позволяет определить наличие и силу связи между двумя или более переменными. Основной показатель, рассчитываемый при корреляционном анализе, – коэффициент корреляции. Он принимает значения от -1 до +1, где:

• +1 означает абсолютную положительную корреляцию (при увеличении одной переменной другая также увеличивается).
• 0 означает отсутствие линейной корреляции (переменные не связаны).
• -1 означает абсолютную отрицательную корреляцию (при увеличении одной переменной другая уменьшается).

Важно понимать, что корреляция указывает только на наличие статистической взаимосвязи, но не на причинно-следственную связь. Две переменные могут сильно коррелировать друг с другом, но это не обязательно означает, что изменение одной вызывает изменение другой.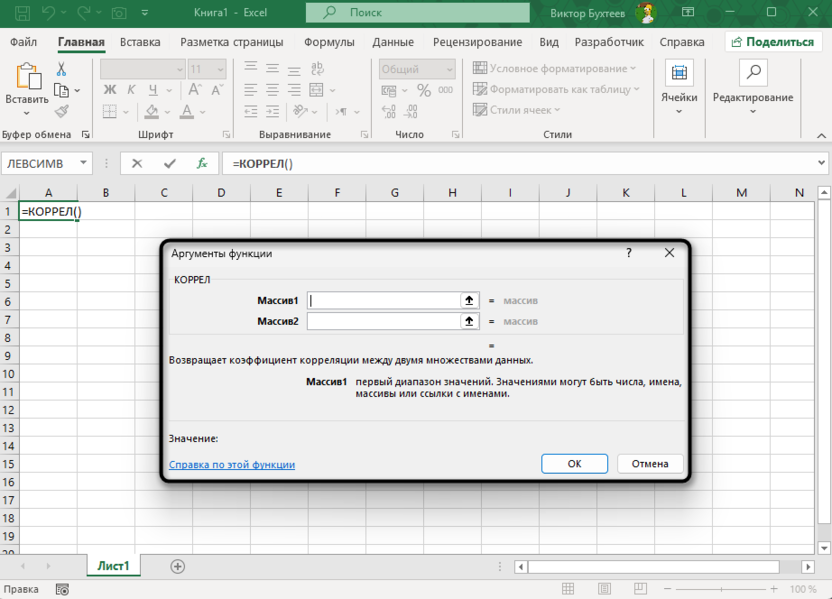

В Excel доступно несколько способов проведения корреляционного анализа: через встроенные функции (КОРРЕЛ), с помощью инструмента «Анализ данных» или путем расчета по формуле. Выбор метода зависит от конкретной задачи, объема данных и требуемой детализации результатов.

Таблица данных для примеров

Для демонстрации возможностей корреляционного анализа в Excel создадим таблицу с данными, которые встречаются в реальных аналитических задачах. Представим, что мы анализируем факторы, влияющие на объем продаж в различных магазинах сети.

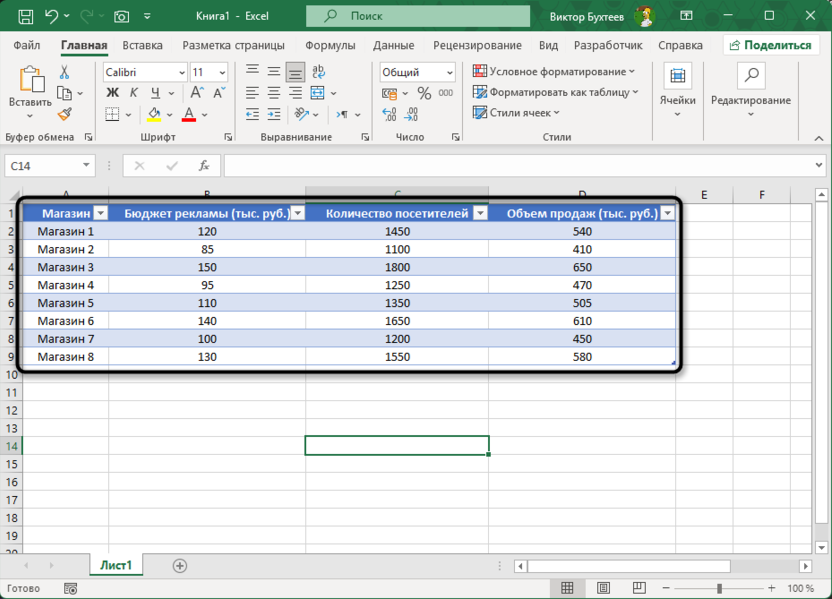
Данная таблица отражает типичную ситуацию в бизнес-анализе, когда необходимо понять влияние различных факторов на ключевые показатели эффективности. В нашем примере мы исследуем связь между рекламным бюджетом, количеством посетителей и объемом продаж в разных магазинах сети. Это поможет руководству принимать более обоснованные решения о распределении рекламных бюджетов и оптимизации работы магазинов для увеличения продаж.

Пример 1: Использование функции КОРРЕЛ для расчета парной корреляции

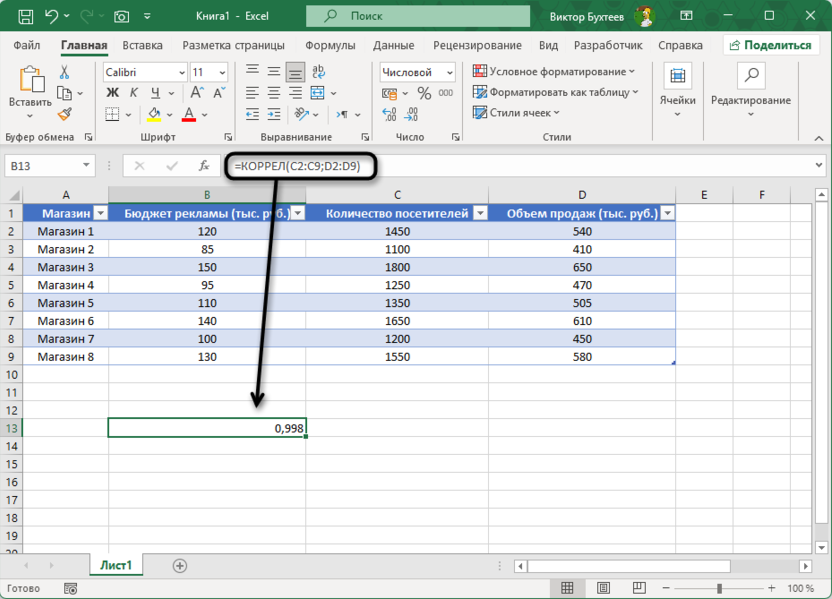
Наиболее простой способ рассчитать коэффициент корреляции между двумя наборами данных – использовать функцию КОРРЕЛ. Начнем с анализа взаимосвязи между рекламным бюджетом и объемом продаж, чтобы определить, насколько эффективны маркетинговые инвестиции.

=КОРРЕЛ(B2:B9;D2:D9)

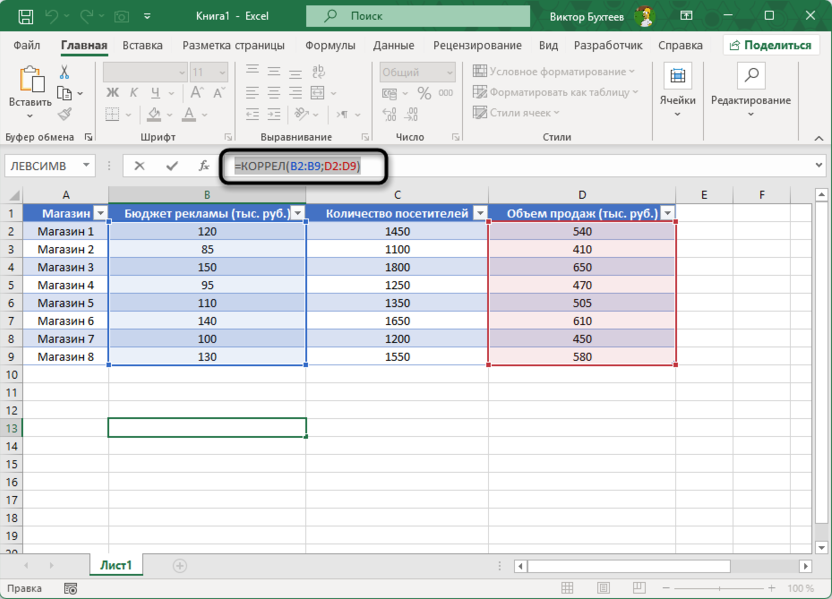
В этой формуле B2:B9 – диапазон с данными по рекламным бюджетам, а D2:D9 – диапазон с данными по объемам продаж. Результат функции будет примерно 0,99, что указывает на очень сильную положительную корреляцию между рекламным бюджетом и объемом продаж.

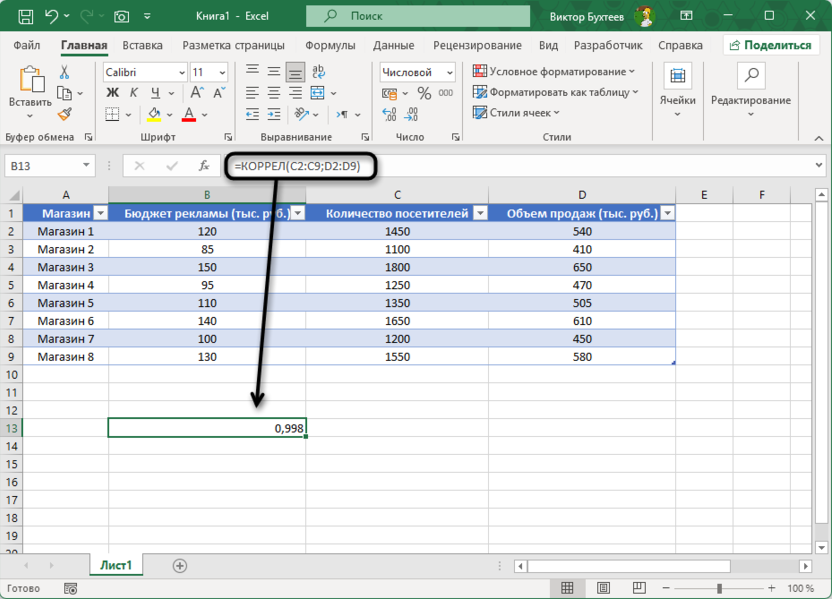
Такой высокий показатель корреляции свидетельствует о том, что увеличение рекламного бюджета практически всегда сопровождается пропорциональным ростом продаж в рассматриваемых магазинах. Для маркетологов и руководителей сети это важная информация, подтверждающая эффективность рекламных инвестиций и обосновывающая дальнейшие вложения в продвижение. При этом стоит помнить о необходимости проверки других факторов, которые могут влиять на данную зависимость.

Пример 2: Анализ корреляции между количеством посетителей и продажами

Теперь рассмотрим, насколько количество посетителей связано с объемом продаж. Этот анализ поможет понять, насколько эффективно магазины конвертируют трафик в реальные продажи.

=КОРРЕЛ(C2:C9;D2:D9)

Здесь C2:C9 – диапазон с данными по количеству посетителей, а D2:D9 – диапазон с данными по объемам продаж. Результат также будет около 0,99, что указывает на очень сильную положительную корреляцию.

Столь высокая корреляция между посещаемостью и продажами показывает, что конверсия посетителей в покупателей происходит достаточно стабильно во всех магазинах сети. Для менеджеров по продажам это сигнал о том, что увеличение трафика является надежным способом повышения выручки. 

Однако стоит дополнительно проанализировать коэффициент конверсии (отношение продаж к числу посетителей) для каждого магазина, чтобы выявить лидеров и отстающих по этому показателю и найти возможности для улучшения.

Пример 3: Построение корреляционной матрицы с помощью Анализа данных

Когда требуется проанализировать взаимосвязи между несколькими переменными одновременно, удобнее использовать инструмент «Анализ данных» для построения корреляционной матрицы. Эта матрица показывает коэффициенты корреляции между всеми парами переменных. Для построения корреляционной матрицы необходимо:

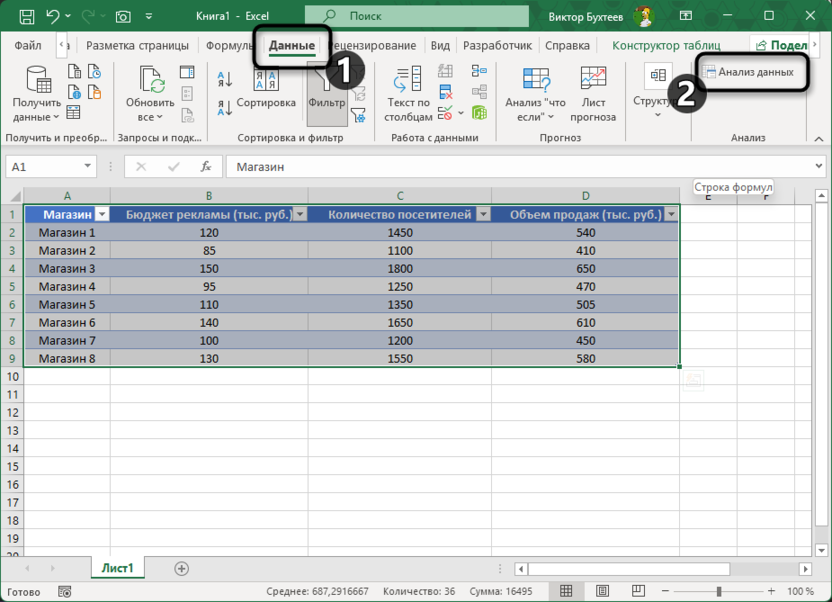
1. Перейти на вкладку «Данные» в Excel. Нажать на кнопку «Анализ данных» (если она отсутствует, нужно сначала включить надстройку «Пакет анализа»).

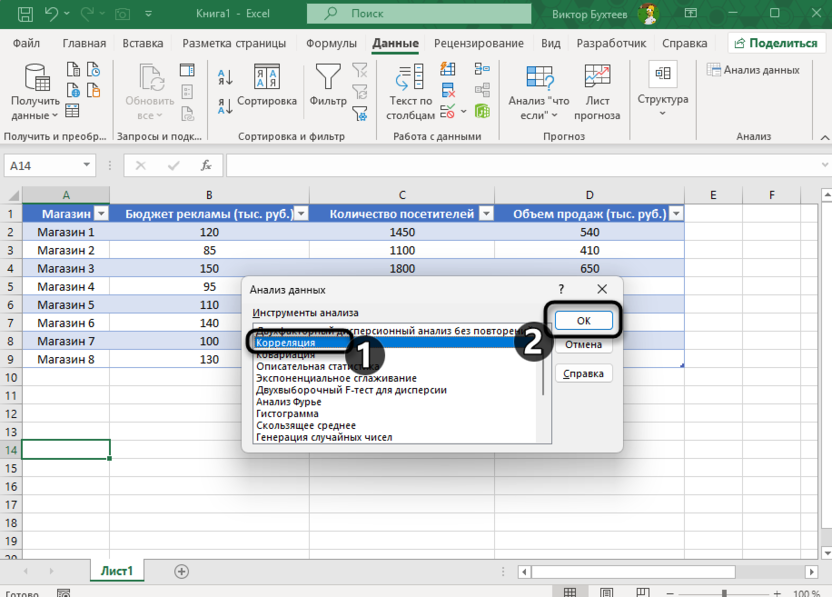
2. В открывшемся окне выбрать «Корреляция» и нажать «OK».

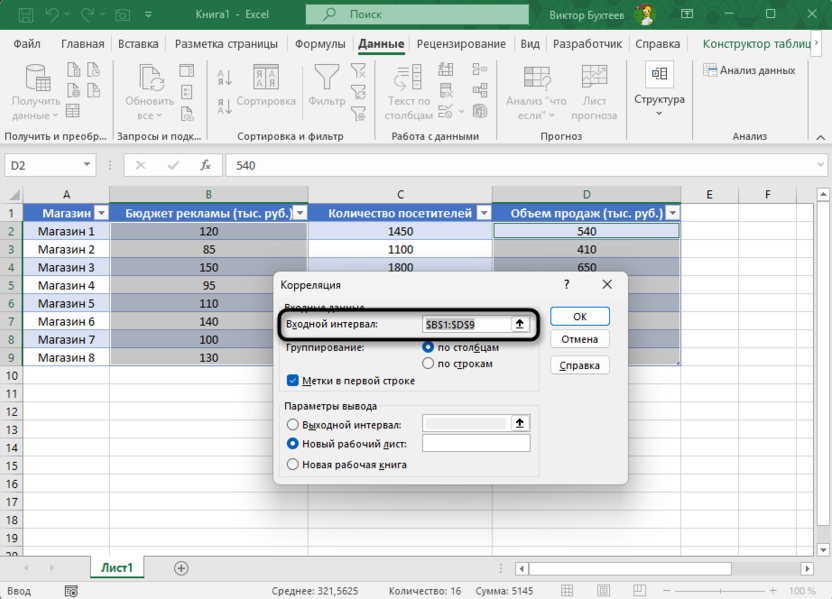
3. В поле «Входной интервал» указать диапазон B1:D9, включающий заголовки столбцов.

4. Установить флажок «Метки в первой строке».

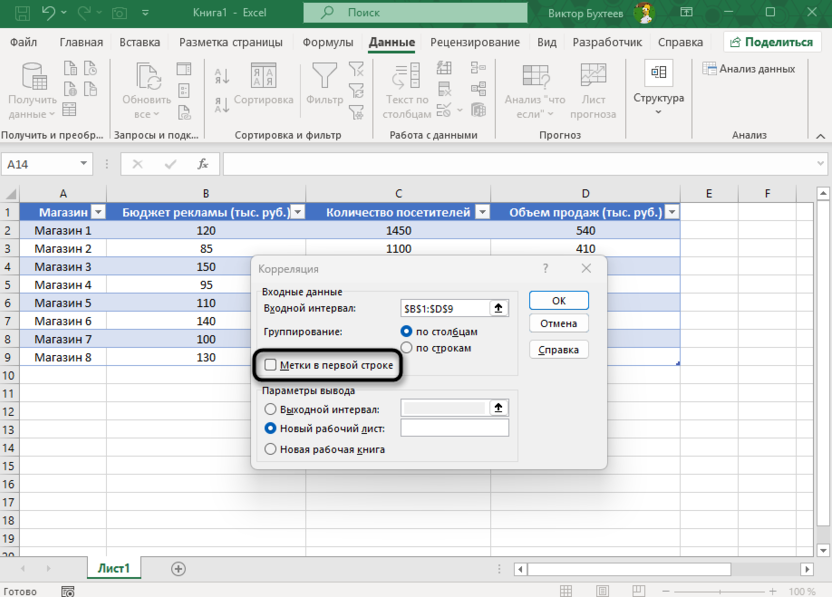
5. Выбрать выходной диапазон или новый лист для результатов. Нажать «OK».

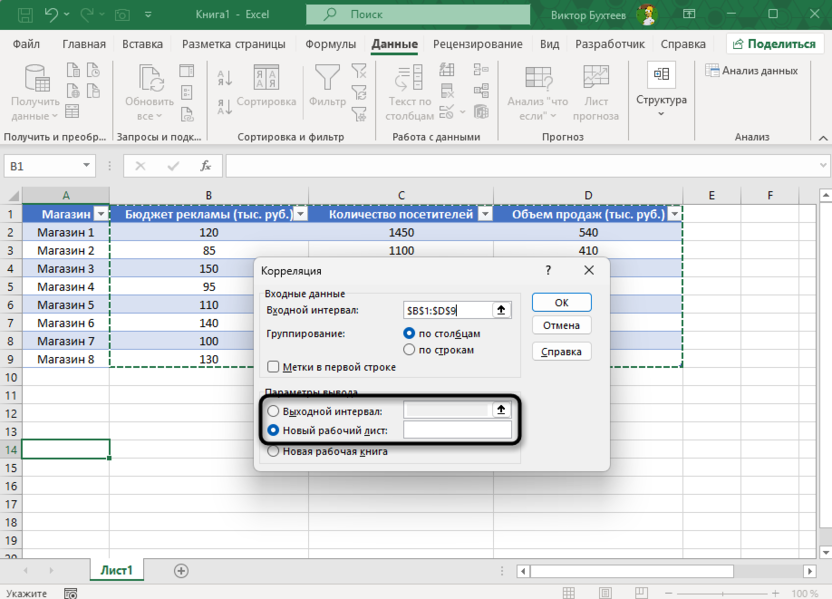
Полученная корреляционная матрица будет иметь следующий вид:

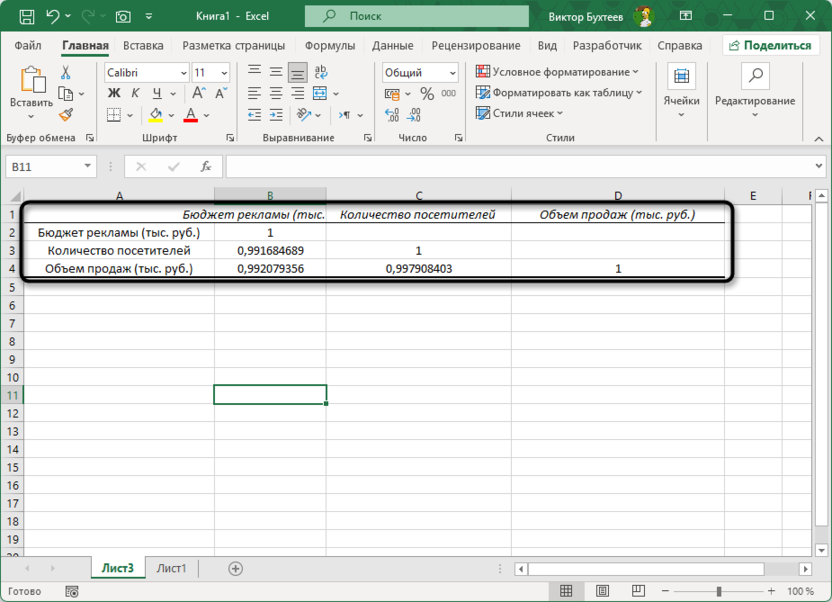
Данная матрица предоставляет комплексное представление о взаимосвязях между всеми исследуемыми переменными. Мы видим, что все три показателя очень сильно коррелируют между собой. Особенно интересна высокая корреляция (0,99) между бюджетом рекламы и количеством посетителей, что указывает на высокую эффективность рекламных кампаний в привлечении клиентов.

Корреляционная матрица становится особенно полезной при анализе большого числа переменных, когда визуальное представление всех парных корреляций позволяет быстро выявить наиболее значимые взаимосвязи и сосредоточиться на них для дальнейшего анализа.

Визуализация корреляции с помощью диаграммы рассеяния

Для наглядного представления корреляции между переменными можно использовать диаграмму рассеяния (точечную диаграмму). Такая визуализация помогает не только увидеть силу взаимосвязи, но и выявить потенциальные нелинейные зависимости или выбросы.

Для создания диаграммы рассеяния:

1. Выделите данные по рекламному бюджету (B2:B9).

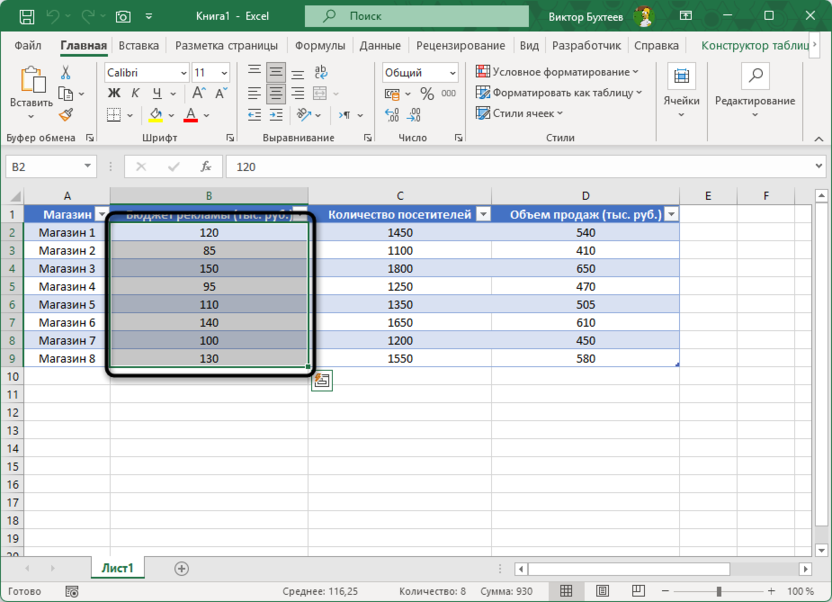
2. Удерживая клавишу Ctrl, выделите данные по объему продаж (D2:D9).

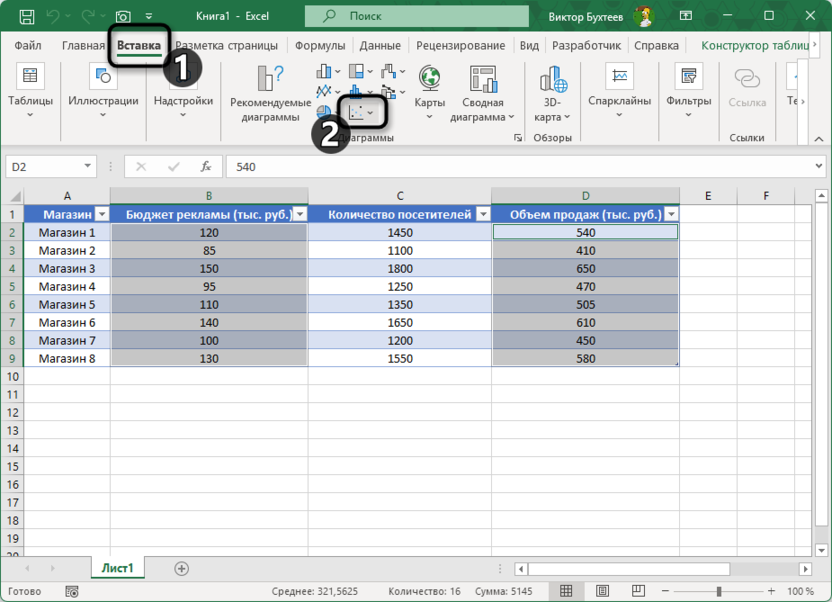
3. Перейдите на вкладку «Вставка» и выберите «Точечная диаграмма».

4. Укажите подходящий для вас тип диаграммы.

Дополнительно можно добавить линию тренда, которая наглядно покажет направление и силу взаимосвязи:

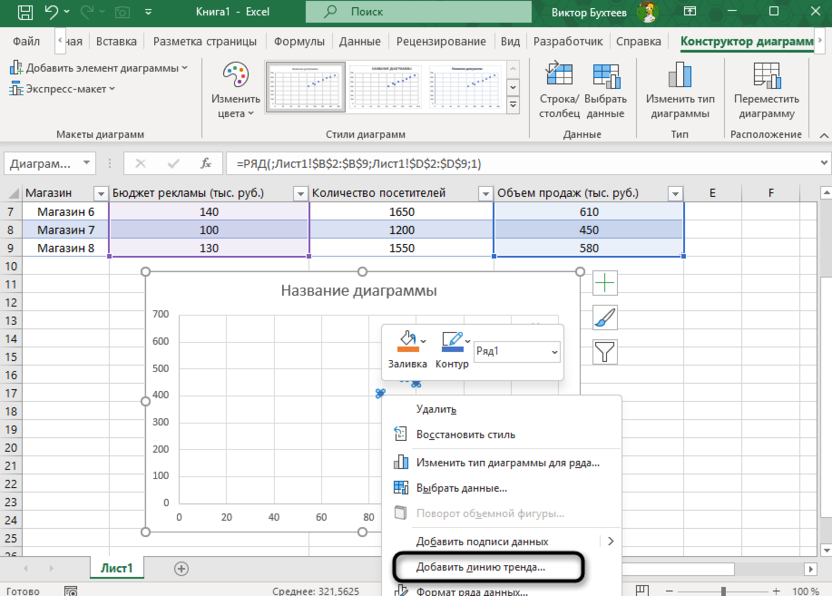
1. Щелкните правой кнопкой мыши по любой точке на диаграмме и выберите «Добавить линию тренда».

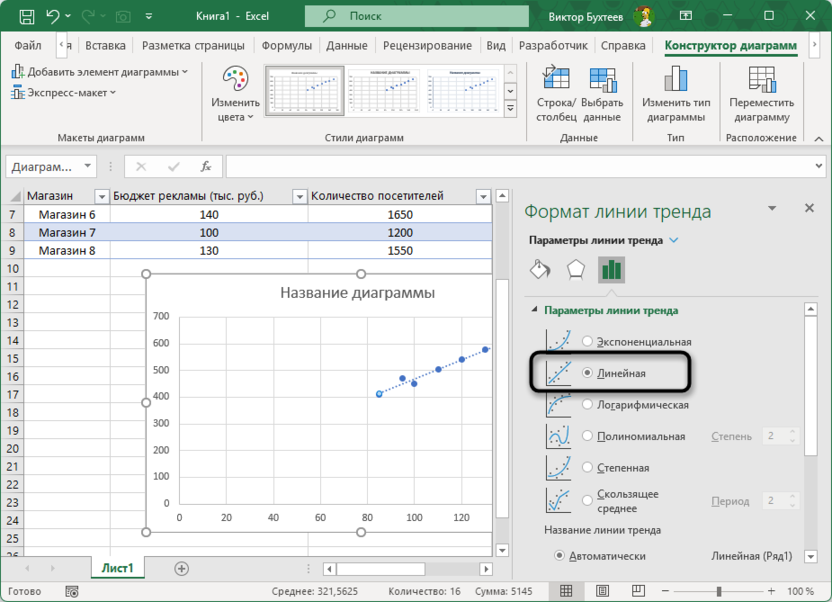
2. Выберите тип линии (обычно линейная). 

3. Установите флажок «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R²)».

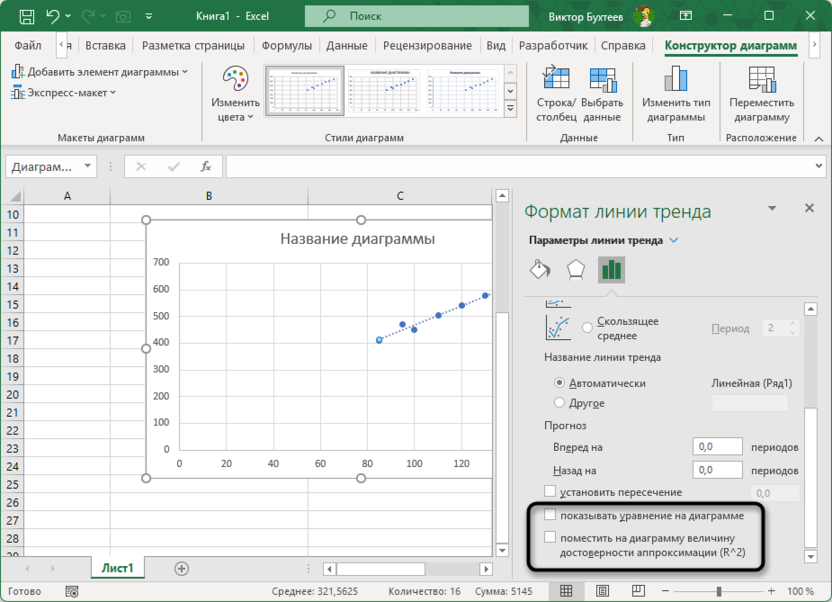
Полученная диаграмма наглядно демонстрирует сильную положительную корреляцию между рекламным бюджетом и объемом продаж. Значение R² (квадрат коэффициента корреляции) показывает, какая доля вариации зависимой переменной (объема продаж) объясняется изменением независимой переменной (рекламного бюджета).

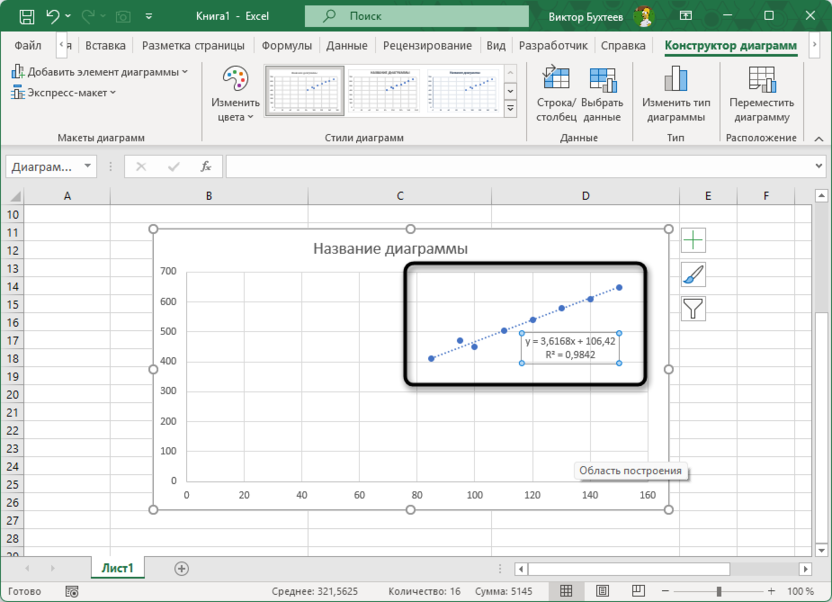
Такая визуализация делает статистическую информацию более доступной для понимания и интерпретации. На диаграмме четко видно, как расположены данные относительно линии тренда, что помогает выявить потенциальные аномалии или паттерны, которые могут быть скрыты при анализе только численных показателей.

Советы по проведению корреляционного анализа в Excel

При работе с корреляционным анализом в Excel важно учитывать несколько ключевых моментов. Во-первых, корреляция не всегда означает причинно-следственную связь – две переменные могут быть связаны через третий фактор или просто случайно коррелировать. Во-вторых, коэффициент Пирсона (который используется в функции КОРРЕЛ) предназначен для выявления линейных зависимостей и может не обнаружить нелинейные связи между переменными.

Также рекомендуется всегда визуализировать данные перед интерпретацией коэффициентов корреляции, так как диаграмма рассеяния может выявить закономерности, не очевидные при анализе только числовых показателей. Важно проверять данные на наличие выбросов – экстремальных значений, которые могут искажать результаты корреляционного анализа.

При наличии временных рядов (например, данных за несколько периодов) стоит учитывать возможность автокорреляции, когда значения переменной коррелируют со своими предыдущими значениями. В таких случаях может потребоваться более сложный статистический анализ.

Заключение

Корреляционный анализ в Excel – возможность для выявления взаимосвязей между различными показателями. Благодаря встроенным функциям и инструментам Excel делает этот статистический метод доступным даже для пользователей без специальной подготовки в области статистики.

Правильное применение корреляционного анализа помогает принимать более обоснованные решения в различных сферах – от маркетинга и продаж до финансового анализа и управления персоналом. При этом важно помнить о ограничениях данного метода и дополнять его другими аналитическими инструментами для получения полной картины.