Microsoft Excel предоставляет широкие возможности для статистического анализа данных, включая вычисление доверительных интервалов. Доверительные интервалы играют важную роль при оценке точности полученных результатов и принятии решений на основе статистических данных.
Они помогают определить диапазон значений, в котором с заданной вероятностью находится истинное значение параметра. Применение доверительных интервалов актуально в различных сферах – от научных исследований до бизнес-аналитики. Excel значительно упрощает расчет этих показателей благодаря встроенным статистическим функциям и инструментам анализа данных.
Что такое доверительный интервал
Доверительный интервал представляет собой диапазон значений, который с определенной вероятностью содержит истинное значение исследуемого параметра. Эта вероятность называется уровнем доверия и обычно выражается в процентах (например, 95% или 99%). Чем выше уровень доверия, тем шире доверительный интервал и тем выше уверенность в том, что истинное значение находится внутри этого интервала.
Для расчета доверительного интервала необходимо знать среднее значение выборки, стандартное отклонение (или стандартную ошибку) и размер выборки. В зависимости от ситуации также используются различные распределения вероятностей, например, нормальное распределение или t-распределение Стьюдента. Последнее чаще применяется для малых выборок, что часто встречается на практике.
Excel предлагает несколько способов вычисления доверительных интервалов: с помощью встроенных функций (ДОВЕРИТ, ДОВЕРИТ.НОРМ, ДОВЕРИТ.СТЬЮДЕНТ), через пакет анализа данных или путем создания собственных формул на основе статистических принципов. Выбор метода зависит от характера данных, размера выборки и требуемой точности анализа.
Таблица данных для примеров
Для наглядной демонстрации вычисления доверительных интервалов создадим таблицу с примером данных, которые часто встречаются в реальных аналитических задачах. Представим, что мы анализируем результаты тестирования эффективности нового препарата, измеряя уровень снижения артериального давления (в мм рт. ст.) у группы пациентов.
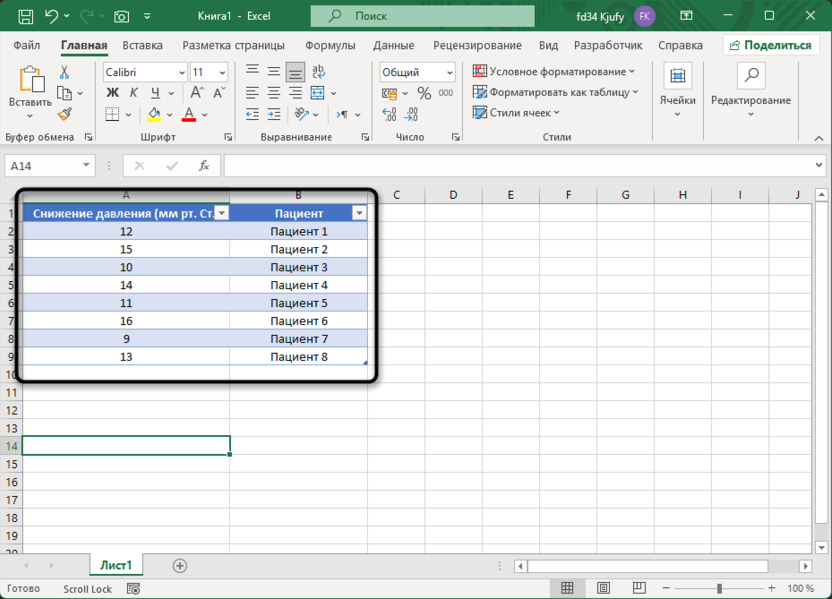
Данная таблица представляет типичную ситуацию в медицинских исследованиях, где необходимо не только определить среднюю эффективность лечения, но и оценить, насколько точно полученные результаты отражают действительность. Малое количество пациентов в нашем примере соответствует пилотному исследованию или начальной фазе клинических испытаний, что делает оценку доверительного интервала особенно важной. Широкий доверительный интервал укажет на необходимость увеличения выборки для получения более надежных результатов.
Пример 1: Использование функции ДОВЕРИТ.СТЬЮДЕНТ
При работе с малыми выборками, как в нашем случае (8 пациентов), для расчета доверительного интервала рекомендуется использовать t-распределение Стьюдента. Функция ДОВЕРИТ.СТЬЮДЕНТ в Excel позволяет рассчитать половину ширины доверительного интервала для заданного уровня доверия.
Сначала рассчитаем среднее значение и стандартное отклонение нашей выборки:
=СРЗНАЧ(A2:9) // Результат: 12,5 (среднее значение снижения давления) =СТАНДОТКЛОН.В(A2:9) // Результат: 2,45 (стандартное отклонение)
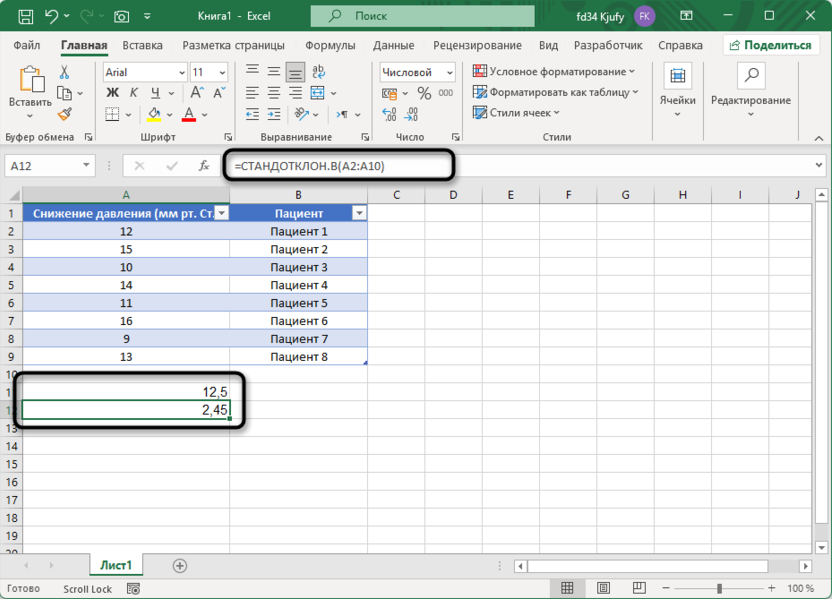
Теперь используем функцию ДОВЕРИТ.СТЬЮДЕНТ для расчета половины ширины доверительного интервала при уровне доверия 95%:
=ДОВЕРИТ.СТЬЮДЕНТ(0,05; 2,45; 8)
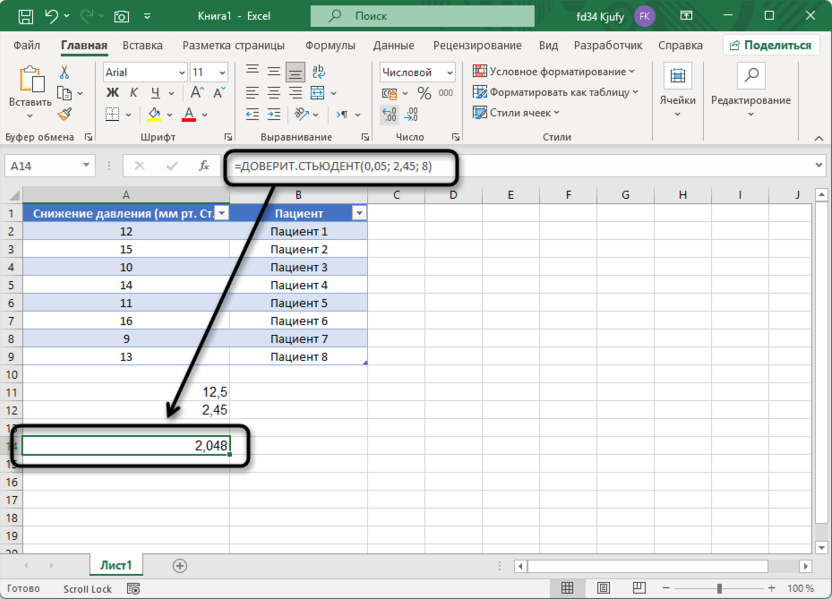
Разберем аргументы функции: 0,05 – это уровень значимости (равный 1 минус уровень доверия, то есть 1 - 0,95 = 0,05); 2,45 – стандартное отклонение выборки; 8 – размер выборки. Выбор уровня значимости 0,05 соответствует 95% доверительному интервалу, что является стандартным в большинстве исследований.
Результатом функции будет значение примерно 2,04. Это означает, что половина ширины доверительного интервала составляет 2,04 мм рт. ст. Полный доверительный интервал рассчитывается как среднее значение ± полученная величина:
Нижняя граница: 12,5 - 2,04 = 10,46 мм рт. ст.
Верхняя граница: 12,5 + 2,04 = 14,54 мм рт. ст.
Таким образом, с 95% уверенностью можно утверждать, что истинное среднее значение снижения давления при применении препарата находится в интервале от 10,46 до 14,54 мм рт. ст. Эта информация критически важна для оценки эффективности лечения и сравнения с другими препаратами.
Пример 2: Использование функции ДОВЕРИТ.НОРМ
Для больших выборок (обычно n ≥ 30) или когда известно, что данные подчиняются нормальному распределению, можно использовать функцию ДОВЕРИТ.НОРМ, которая основана на нормальном распределении. Хотя наша выборка небольшая, рассмотрим этот пример для сравнения результатов.
=ДОВЕРИТ.НОРМ(0,05; 2,45; 8)
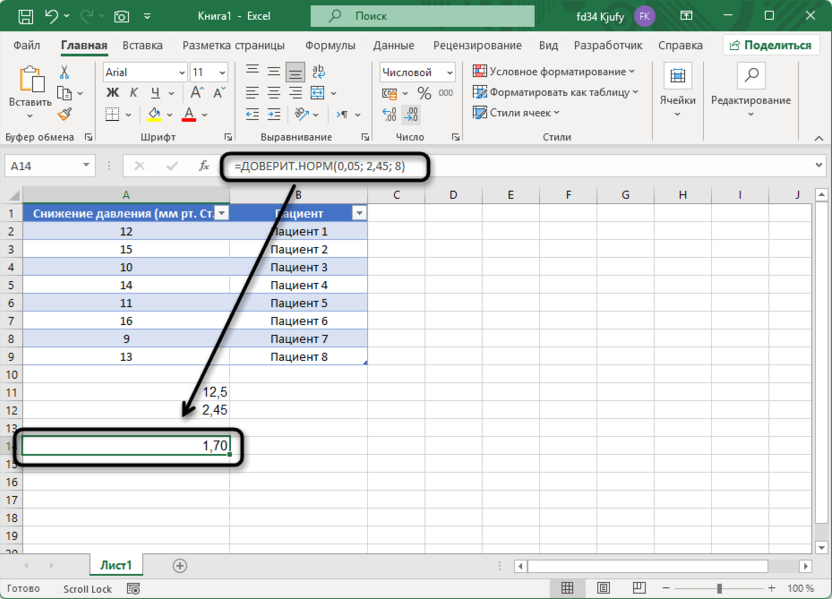
Аргументы те же, что и в предыдущей функции: 0,05 – уровень значимости; 2,45 – стандартное отклонение; 8 – размер выборки. Результат будет примерно 1,7 мм рт. ст., что меньше значения, полученного с использованием t-распределения.
Доверительный интервал при использовании нормального распределения: Нижняя граница: 12,5 - 1,7 = 10,8 мм рт. ст. Верхняя граница: 12,5 + 1,7 = 14,2 мм рт. ст.
Заметно, что доверительный интервал при использовании нормального распределения уже, чем при использовании t-распределения Стьюдента. Это характерная особенность: для малых выборок t-распределение дает более консервативные (широкие) интервалы, учитывая большую неопределенность из-за ограниченного количества наблюдений. Поэтому для нашего примера более корректным является использование функции ДОВЕРИТ.СТЬЮДЕНТ.
Пример 3: Комплексный расчет доверительного интервала с использованием нескольких функций
В практических задачах часто требуется автоматизировать расчет доверительных интервалов, отобразив результаты в удобной форме. Создадим более сложную формулу, которая будет вычислять и верхнюю, и нижнюю границы интервала в одной ячейке.
Формула для нижней границы доверительного интервала:
=СРЗНАЧ(A2:A9)-ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A19); СЧЁТ(A2:A9))
Формула для верхней границы доверительного интервала:
=СРЗНАЧ(A2:A9)+ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9))
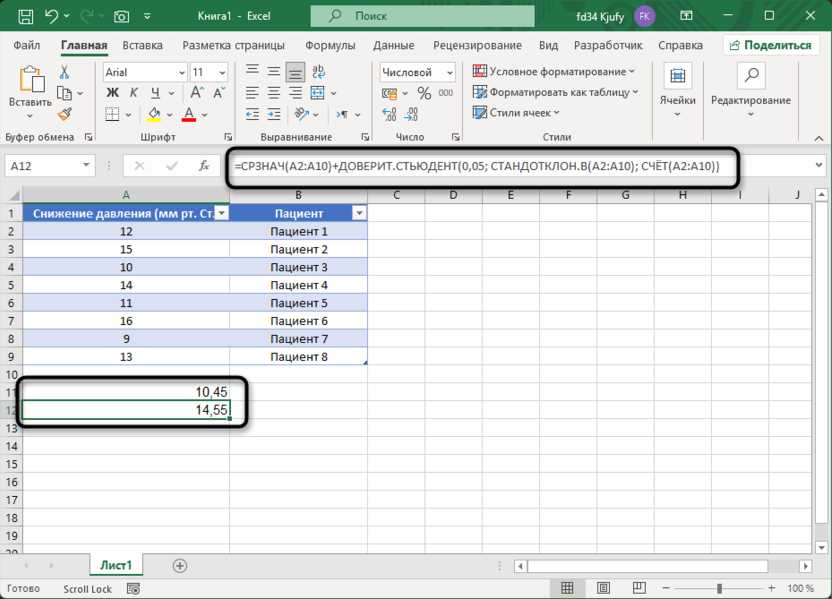
Эти формулы автоматически вычисляют все необходимые параметры: среднее значение выборки, стандартное отклонение и размер выборки. Такой подход удобен тем, что при изменении исходных данных доверительный интервал будет пересчитан автоматически.
Для более наглядного представления результатов можно объединить обе границы в одну строку:
=ОКРУГЛ(СРЗНАЧ(A2:A9);2) & " ± " & ОКРУГЛ(ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " (" & ОКРУГЛ(СРЗНАЧ(A2:A9)-ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " - " & ОКРУГЛ(СРЗНАЧ(A2:A9)+ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & ")"
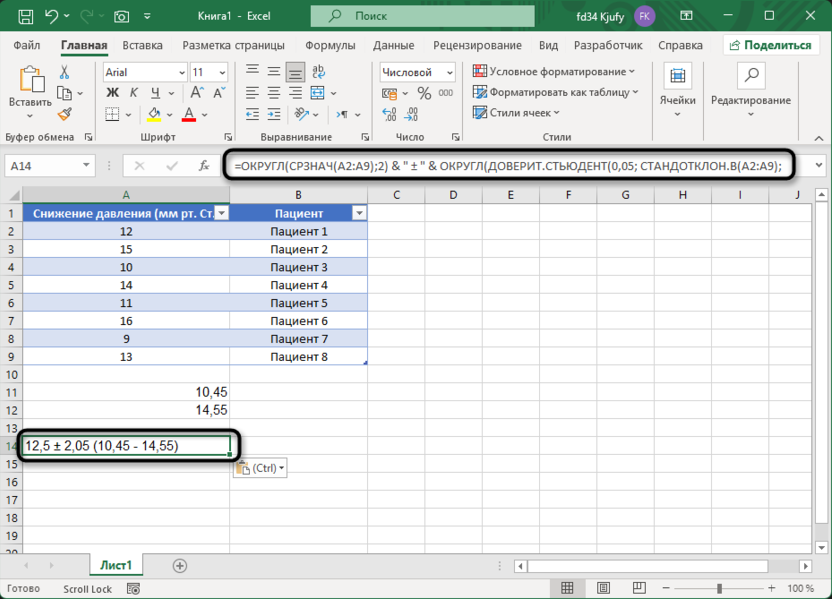
Эта формула выведет результат в формате "12,5 ± 2,04 (10,46 - 14,54)", что соответствует стандартному представлению результатов в научных публикациях. Функция ОКРУГЛ используется для ограничения числа десятичных знаков до двух, что повышает читаемость результатов.
Пример 4: Расчет доверительных интервалов для разных уровней доверия
В некоторых исследованиях требуется сравнить доверительные интервалы для различных уровней доверия. Создадим таблицу, которая показывает доверительные интервалы для уровней доверия 90%, 95% и 99%.
Формула для 90% доверительного интервала (в одну строку):
=ОКРУГЛ(СРЗНАЧ(A2:A9);2) & " ± " & ОКРУГЛ(ДОВЕРИТ.СТЬЮДЕНТ(0,1; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " (" & ОКРУГЛ(СРЗНАЧ(A2:A9)-ДОВЕРИТ.СТЬЮДЕНТ(0,1; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " - " & ОКРУГЛ(СРЗНАЧ(A2:A9)+ДОВЕРИТ.СТЬЮДЕНТ(0,1; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & ")"
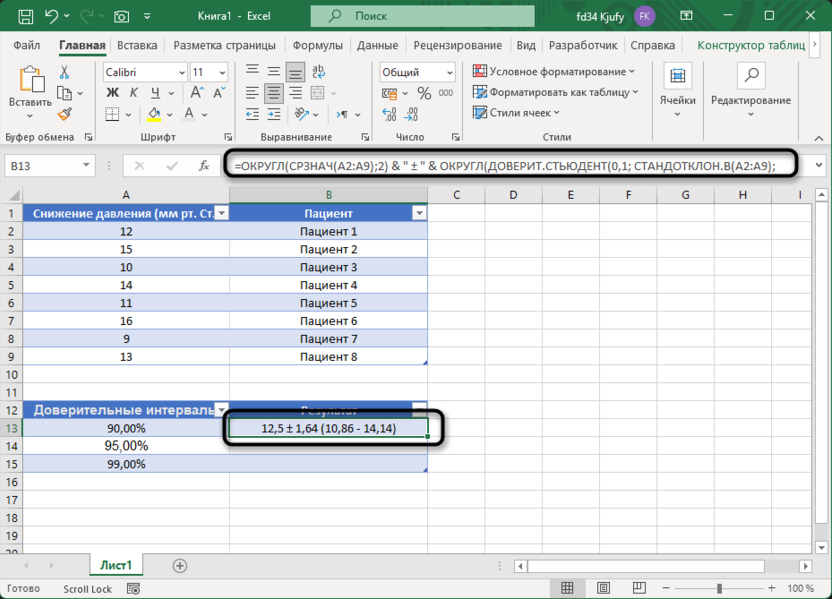
Формула для 95% доверительного интервала (в одну строку):
=ОКРУГЛ(СРЗНАЧ(A2:A9);2) & " ± " & ОКРУГЛ(ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " (" & ОКРУГЛ(СРЗНАЧ(A2:A9)-ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " - " & ОКРУГЛ(СРЗНАЧ(A2:A9)+ДОВЕРИТ.СТЬЮДЕНТ(0,05; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & ")"
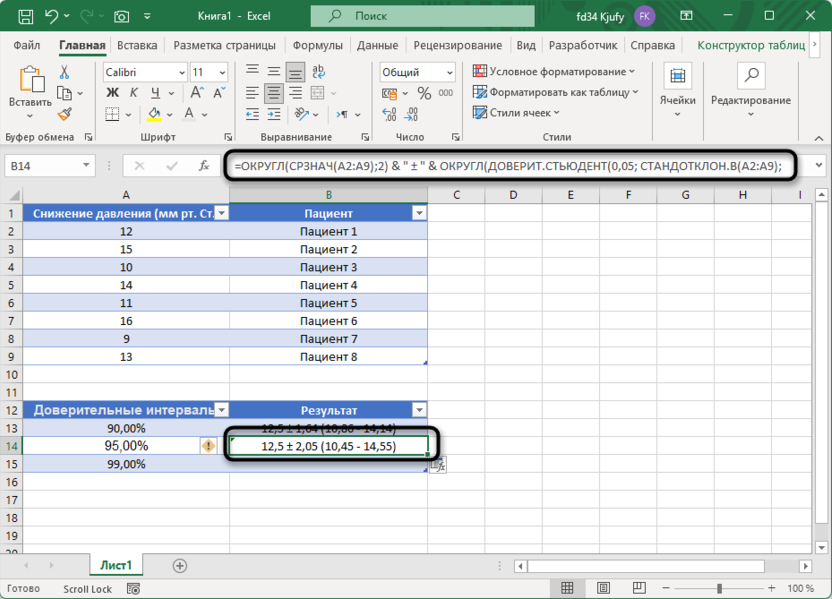
Формула для 99% доверительного интервала (в одну строку):
=ОКРУГЛ(СРЗНАЧ(A2:A9);2) & " ± " & ОКРУГЛ(ДОВЕРИТ.СТЬЮДЕНТ(0,01; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " (" & ОКРУГЛ(СРЗНАЧ(A2:A9)-ДОВЕРИТ.СТЬЮДЕНТ(0,01; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & " - " & ОКРУГЛ(СРЗНАЧ(A2:A9)+ДОВЕРИТ.СТЬЮДЕНТ(0,01; СТАНДОТКЛОН.В(A2:A9); СЧЁТ(A2:A9));2) & ")"
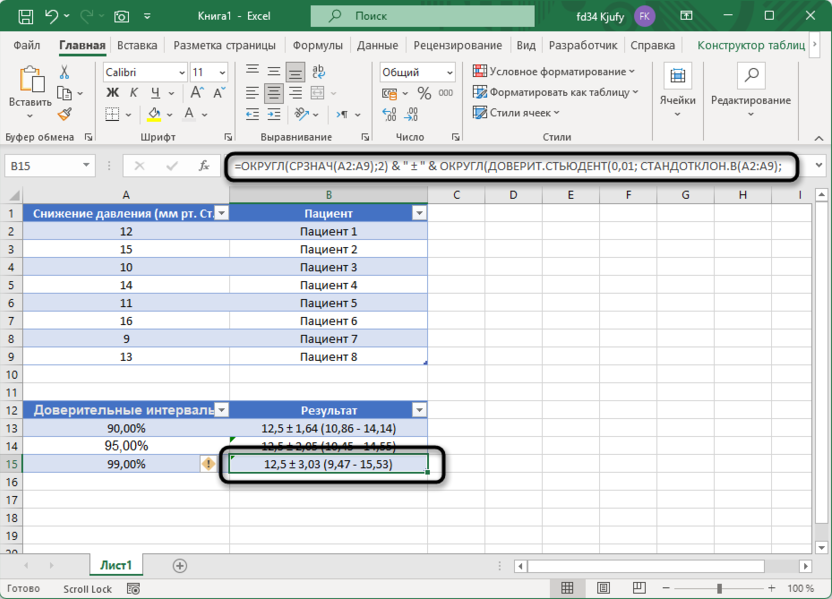
Обратите внимание на изменение первого аргумента функции ДОВЕРИТ.СТЬЮДЕНТ: 0,1 соответствует 90% доверительному интервалу, 0,05 – 95%, а 0,01 – 99%. Результаты показывают, как ширина доверительного интервала увеличивается с повышением уровня доверия:
90% доверительный интервал: 12,5 ± 1,67 (10,86 - 14,14).
95% доверительный интервал: 12,5 ± 2,04 (10,45 - 14,55).
99% доверительный интервал: 12,5 ± 2,82 (9,47 - 15,53).
В Excel значения доверительных интервалов могут незначительно отличаться от ручных расчетов из-за особенностей округления и точности используемых критических значений t-распределения. Excel автоматически интерполирует значения для нужных степеней свободы, что может давать чуть отличающиеся результаты по сравнению с таблицами в учебниках или статических расчетах. Эти различия, как правило, минимальны и не влияют на общую интерпретацию, поэтому при использовании встроенных функций Excel такие расхождения считаются допустимыми и безопасными для анализа.
Советы по использованию доверительных интервалов в Excel
При работе с доверительными интервалами в Excel полезно учитывать несколько рекомендаций. Во-первых, всегда учитывайте размер выборки при выборе метода расчета – используйте t-распределение для малых выборок и нормальное распределение для больших. Во-вторых, при представлении результатов указывайте не только границы интервала, но и использованный уровень доверия, так как без этой информации интерпретация результатов будет неполной.
Также стоит помнить, что функция ДОВЕРИТ без суффикса является устаревшей и сохранена в Excel только для обратной совместимости. Рекомендуется использовать более современные функции ДОВЕРИТ.НОРМ и ДОВЕРИТ.СТЬЮДЕНТ.
При анализе данных с выбросами (экстремальными значениями) рассмотрите возможность применения робастных методов оценки или предварительной очистки данных, так как доверительные интервалы чувствительны к аномальным наблюдениям.
Заключение
Расчет доверительных интервалов в Excel – относительно сложный, но полезный инструмент статистического анализа, доступный даже пользователям без глубоких знаний в области статистики. Функции ДОВЕРИТ.СТЬЮДЕНТ и ДОВЕРИТ.НОРМ, а также возможность создания комплексных формул позволяют быстро оценить точность статистических выводов и представить результаты в профессиональном формате.
Правильное использование доверительных интервалов помогает принимать обоснованные решения в различных областях – от медицинских исследований до контроля качества производственных процессов и маркетингового анализа. Excel делает эти расчеты доступными и наглядными, что значительно упрощает статистический анализ данных в повседневной практике.












Комментарии