Коэффициент детерминации в Excel: что это и как его рассчитать

Коэффициент детерминации (или R2 (2 тут и далее – квадрат) – один из ключевых показателей, используемых в статистике и анализе данных. Он показывает, насколько хорошо модель объясняет изменчивость зависимой переменной. В Excel этот коэффициент можно вычислить разными способами, и важно правильно понимать, что он собой представляет и как его применить на практике.

Что такое коэффициент детерминации

Коэффициент детерминации измеряет степень соответствия модели реальным данным. Он показывает, какую долю вариаций зависимой переменной можно объяснить независимой переменной или переменными. Этот показатель может принимать значения от 0 до 1, где:

• 0 означает, что модель совершенно не объясняет вариации данных.
• 1 означает, что модель идеально предсказывает зависимости.

Если R2 приближается к 1, это указывает на высокую степень соответствия данных модели, в то время как низкие значения говорят о том, что модель плохо объясняет зависимости. Рассчитывая коэффициент детерминации в Excel, вы можете оценить качество ваших прогнозов и линейных моделей.

Пример данных для расчета

Далее я буду демонстрировать пример работы всех способов на уже готовой выборке данных, которую вы видите на следующем изображении. Отталкивайтесь от него, а также учитывайте, какие ячейки или их массивы будут использоваться при составлении последующих формул. Соответственно, в ваших ситуациях их нужно будет редактировать под имеющиеся в таблице массивы.

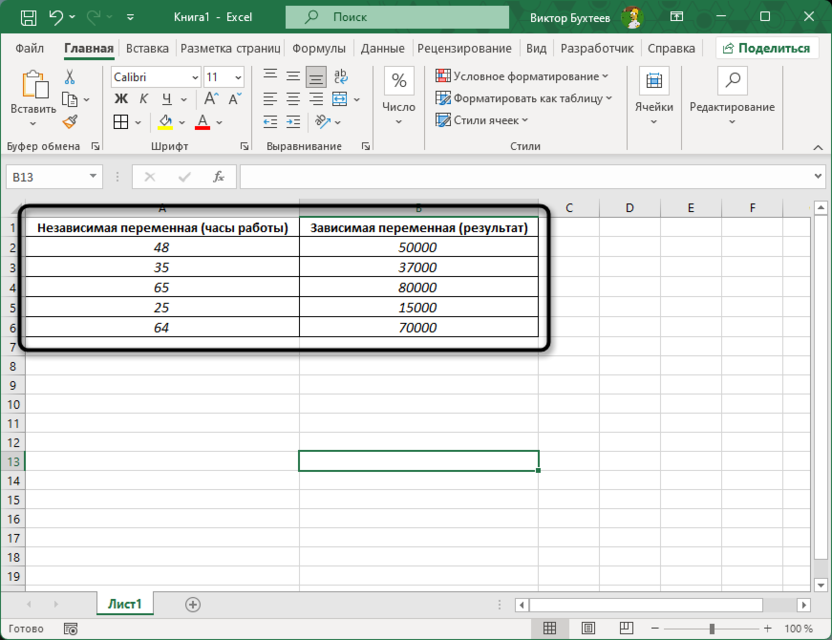
Этот набор данных представляет собой простую зависимость между двумя переменными, где столбец A содержит значения независимой переменной (например, количество часов работы), а столбец B – зависимой переменной (например, результат работы). Эти данные будут использоваться во всех дальнейших методах расчета коэффициента детерминации.

Использование функции КВПИРСОН для вычисления коэффициента детерминации

Первый способ основан на использовании функции КВПИРСОН, которая рассчитывает коэффициент корреляции Пирсона между двумя наборами данных. Коэффициент корреляции показывает, насколько сильно одна переменная связана с другой. После вычисления корреляции, ее возведение в квадрат даст нам коэффициент детерминации R2, который и объясняет, насколько хорошо независимая переменная предсказывает зависимую.

В данном методе вам нужно будет найти коэффициент корреляции между независимой и зависимой переменными, а затем преобразовать его в коэффициент детерминации. Этот способ особенно полезен, если требуется быстро определить силу связи между переменными.

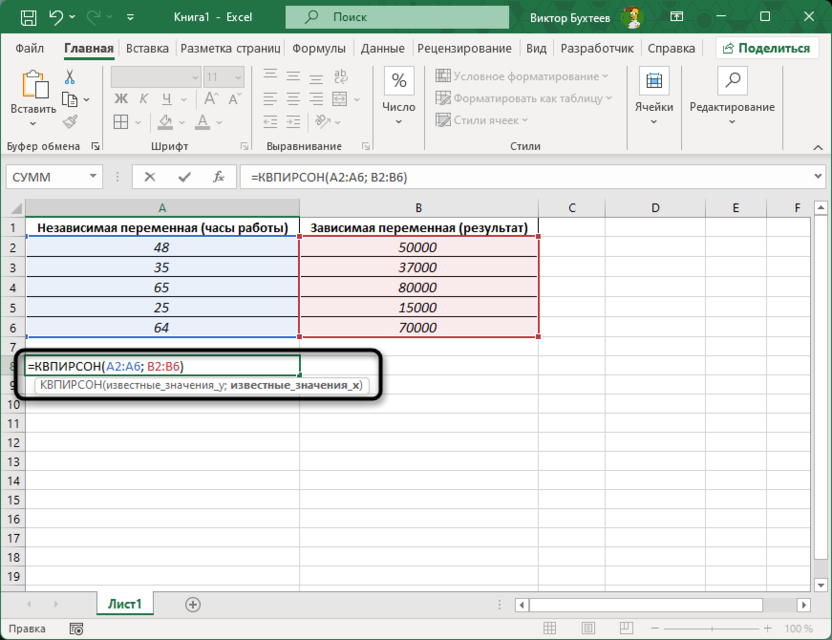
1. Для начала необходимо вычислить коэффициент корреляции между двумя колонками данных. Это можно сделать с помощью формулы =КВПИРСОН(A2:A6; B2:B6).

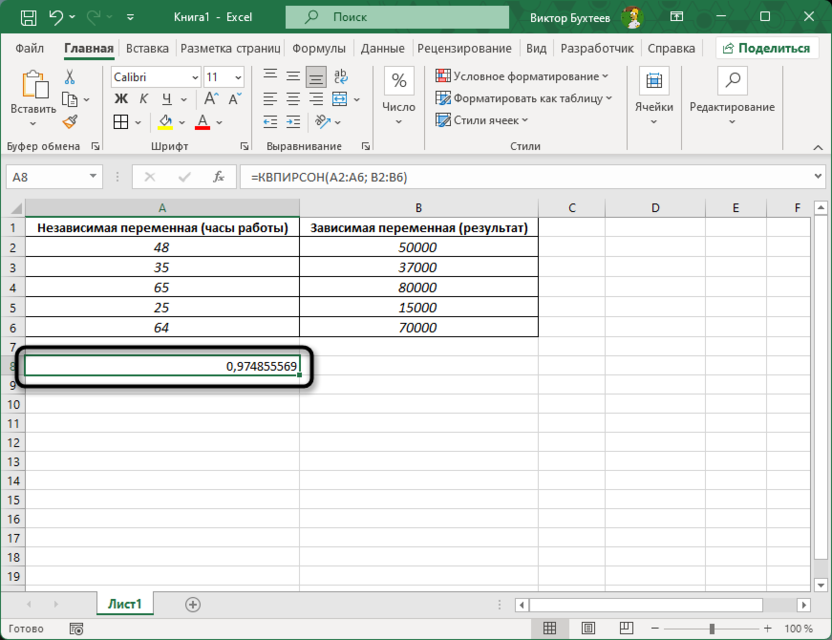
2. Формула КВПИРСОН возвращает значение корреляции между двумя массивами данных, которое находится в пределах от -1 до 1. Положительное значение указывает на прямую зависимость (когда увеличение одной переменной ведет к увеличению другой), отрицательное – на обратную зависимость, а 0 указывает на отсутствие связи между переменными.

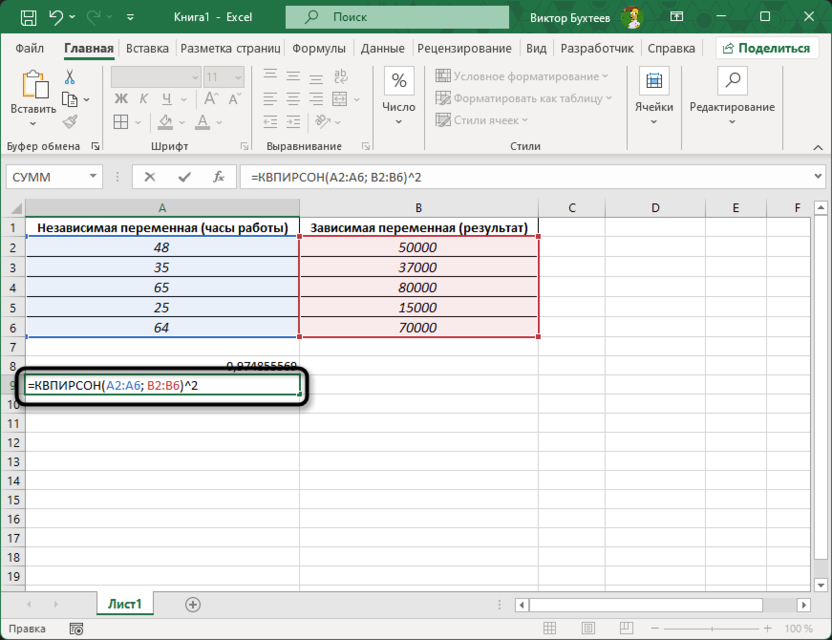
3. После того как коэффициент корреляции получен, следующий шаг – возвести это значение в квадрат, чтобы получить R2. Для этого можно воспользоваться такой формулой =КВПИРСОН(A2:A6; B2:B6)^2.

4. Результат, который вы получите, и будет коэффициентом детерминации R2. Он будет находиться в диапазоне от 0 до 1, где значение, близкое к 1, указывает на сильную зависимость, а значение, близкое к 0, на слабую.

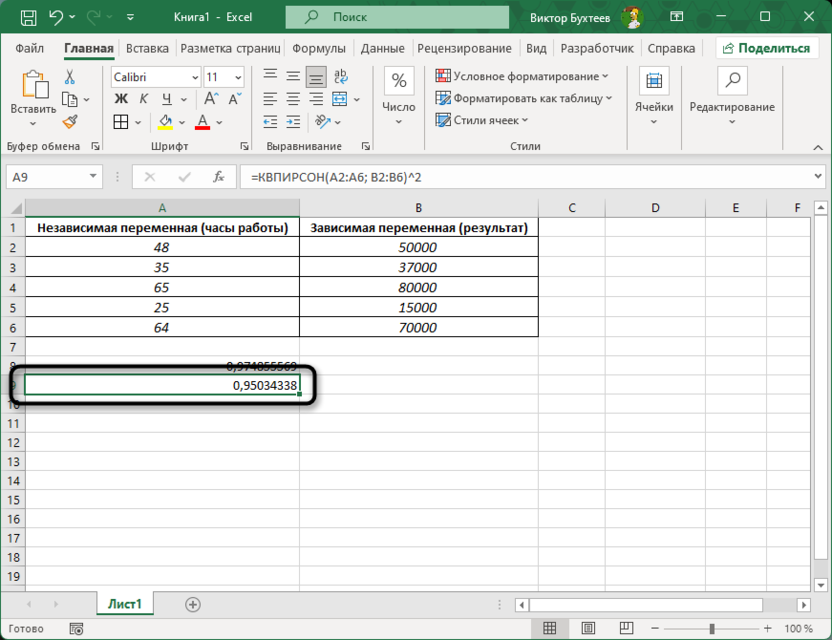
Коэффициент детерминации R2 показывает, какую долю изменений в зависимой переменной можно объяснить изменениями независимой переменной. Например, если R2 равен 0.72, это означает, что 72% изменений зависимой переменной объясняются изменениями независимой переменной.

Преимущества этого метода:

• Простота: использование функции КВПИРСОН требует лишь двух аргументов – диапазона независимых и зависимых переменных.
• Быстрота: результат получается мгновенно, и его можно легко преобразовать в коэффициент детерминации.
• Ясность: коэффициент корреляции Пирсона предоставляет дополнительную информацию о направлении и силе связи между переменными.

Данный подход может быть особенно полезен, если вы хотите быстро получить представление о зависимости между переменными и оценить точность предсказания зависимой переменной на основе независимой.

Использование функции ЛИНЕЙН для вычисления коэффициента детерминации

Функция ЛИНЕЙН в Excel позволяет рассчитать параметры линейной регрессии, включая коэффициент детерминации R2. Это один из наиболее точных методов, так как он предоставляет не только сам коэффициент, но и другие параметры, которые могут быть полезны при анализе данных.

В этом методе вам нужно будет рассчитать линейную зависимость между двумя переменными и получить полный набор результатов, включая коэффициент детерминации. Это позволит понять, насколько хорошо независимая переменная (например, количество часов работы) объясняет зависимую переменную (результат работы).

1. Для получения коэффициента детерминации необходимо воспользоваться функцией ЛИНЕЙН. Эта функция может вернуть полный набор параметров регрессии, включая R2. Для этого введите формулу =ЛИНЕЙН(B2:B6; A2:A6; ИСТИНА; ИСТИНА) в любую пустую ячейку, например, в ячейку D1. Первый аргумент ИСТИНА указывает на то, что нужно включить точку пересечения оси. Второй аргумент ИСТИНА возвращает дополнительные статистические данные, включая R2.

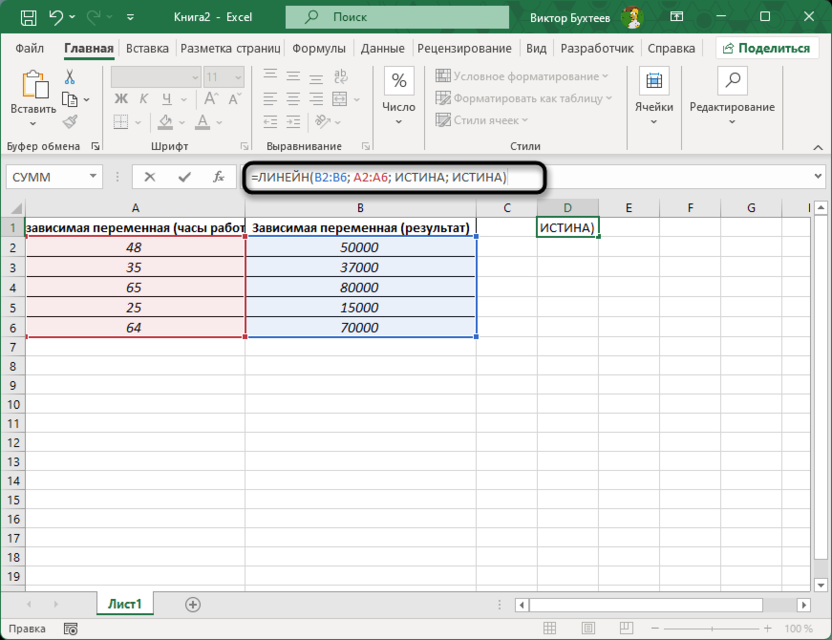
2. После ввода формулы нажмите Ctrl+Shift+Enter, так как это массивная функция. Excel выведет несколько значений. 

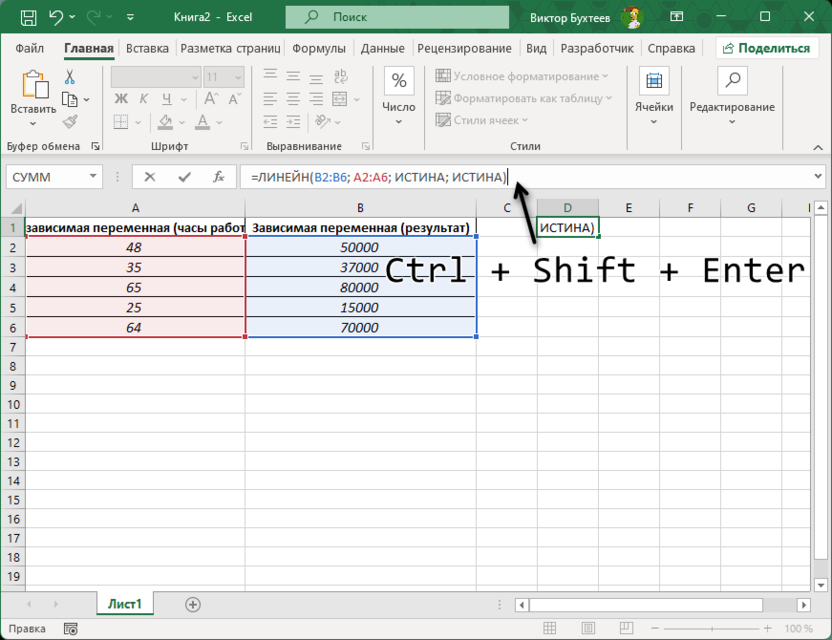
3. Коэффициент детерминации R2 будет находиться в третьей ячейке вывода массива. Например, если формула введена в ячейку D1, коэффициент детерминации появится в ячейке D3.

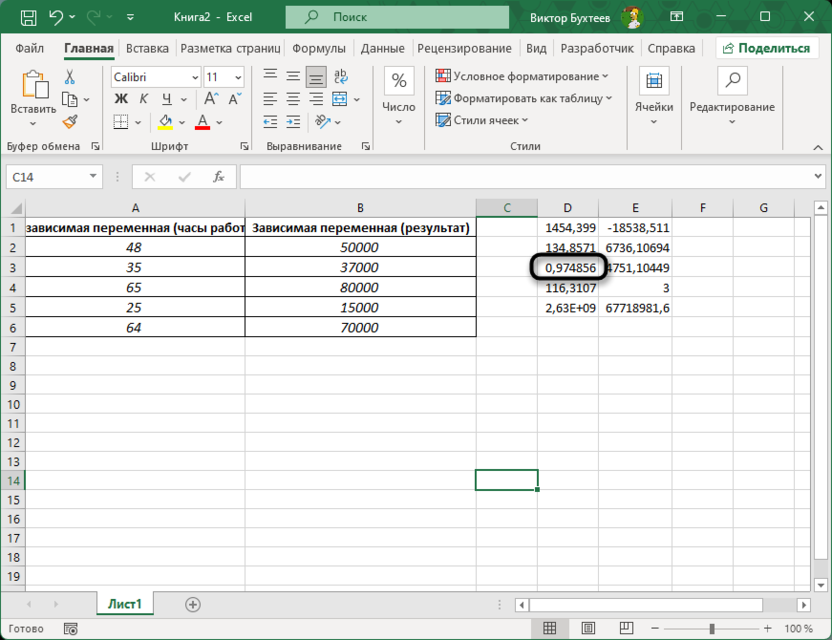
Таким образом, R2 будет равен тому числу, которое Excel выводит в этой ячейке, и оно покажет, какую долю изменений зависимой переменной можно объяснить изменениями независимой.

Преимущества этого метода:

• Точность: функция ЛИНЕЙН предоставляет не только коэффициент детерминации, но и другие важные параметры регрессии, такие как коэффициенты и стандартные ошибки.
• Многофункциональность: этот метод позволяет оценить, насколько хорошо модель линейной регрессии подходит для ваших данных.
• Дополнительная информация: помимо R2, функция возвращает такие параметры, как наклон линии и точка пересечения осей, что может быть полезно для более глубокого анализа.

Этот способ идеально подходит для тех, кто хочет не только рассчитать коэффициент детерминации, но и получить дополнительные статистические данные о зависимости между переменными.

Использование диаграммы с добавлением линии тренда

Для тех, кто предпочитает визуальные методы анализа, построение диаграммы с линией тренда и отображением коэффициента детерминации – это наглядный и простой способ. Построение графика зависимости данных с линией тренда позволит не только увидеть направление изменения, но и получить визуальную оценку качества модели через отображение R2 прямо на диаграмме.

1. Для удобства можете конвертировать исходные данные в таблицу. Для этого выделите диапазон, перейдите на вкладку «‎Вставка» и разверните меню «‎Таблицы».

2. Далее преобразуйте диапазон данных в обычную таблицу.

3. Теперь можете снова выделить ее, а на вкладке «‎Вставка» выбрать одну из подходящих для ваших данных диаграмм.

4. Редактируйте внешний вид и обозначения на диаграмме нужным вам образом. После этого обязательно выделите ее ЛКМ, чтобы отобразилась вкладка «‎Конструктор диаграмм».

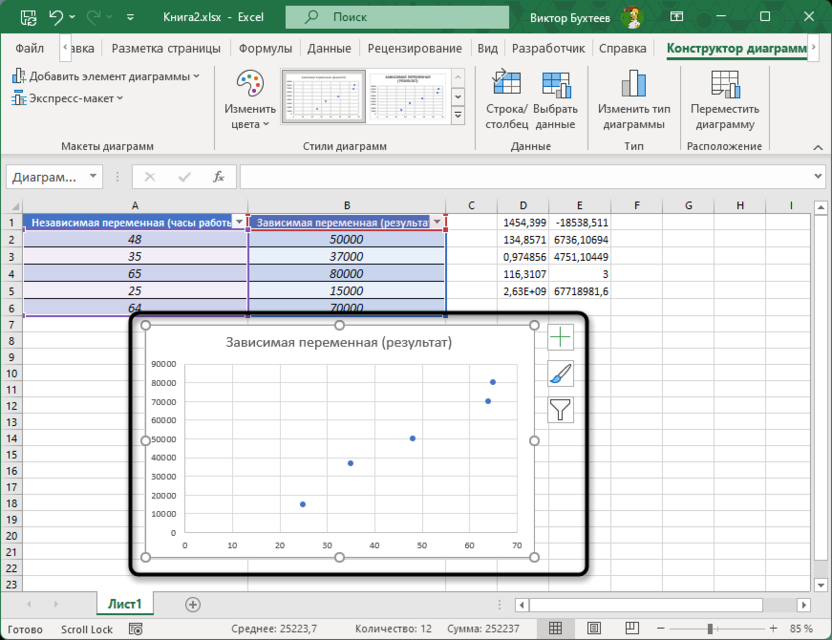
5. На этой вкладке разверните меню «‎Добавить элемент диаграммы», наведите курсор на «‎Линия тренда» и выберите вариант «‎Экспоненциальная».

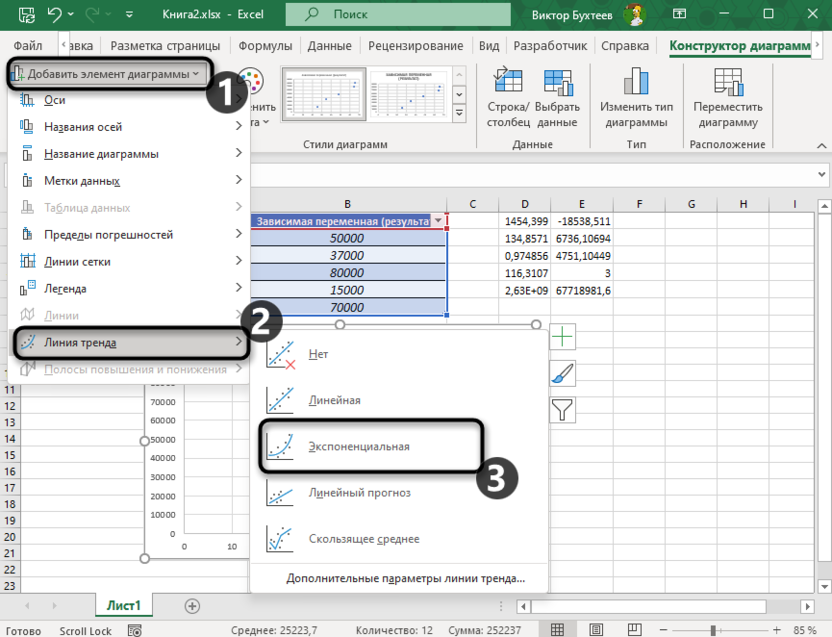
6. Добавится новая линия тренда на ваш график, по которой следует кликнуть ПКМ. Из появившегося контекстного меню выберите пункт «Формат линии тренда‎».

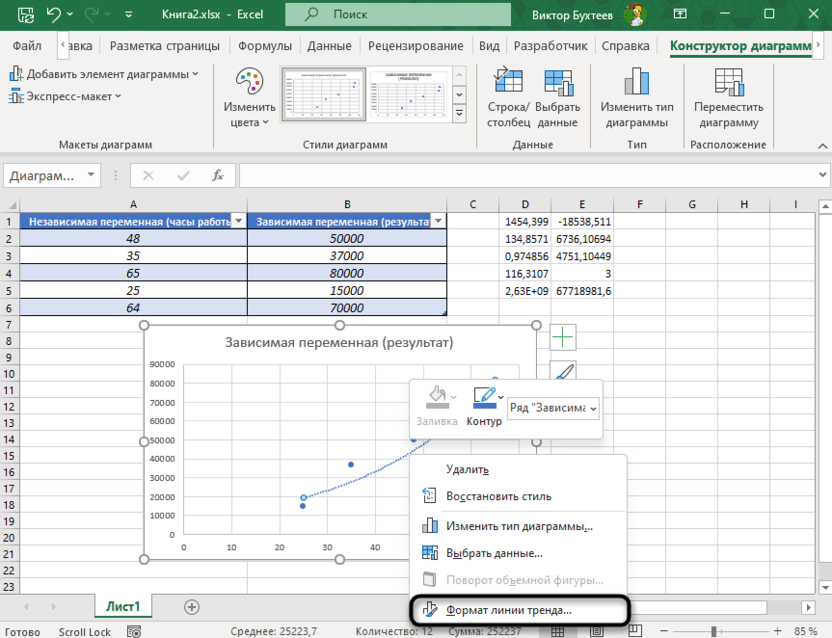
7. Поставьте галочку возле пункта «‎Поместить на диаграмму величину достоверности аппроксимации (R^2)».

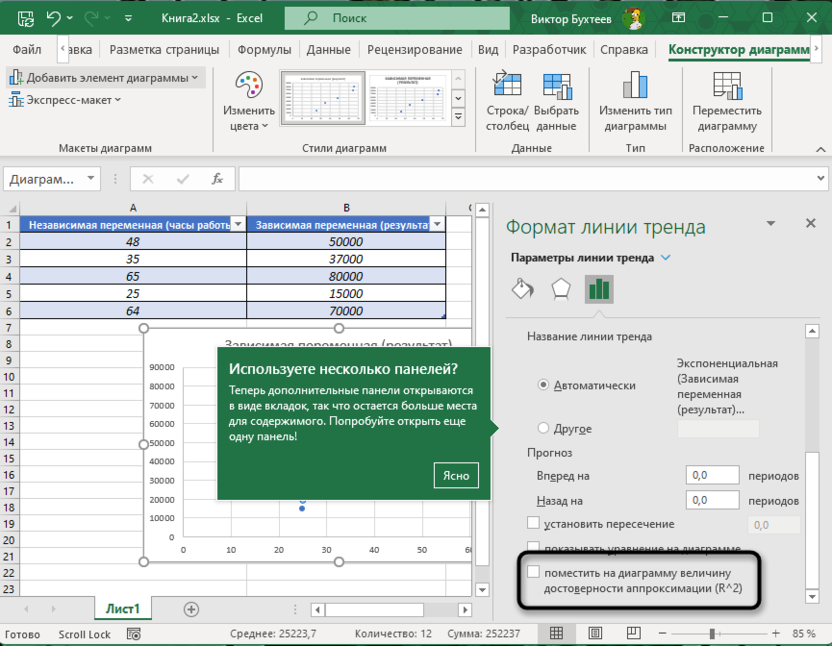
8. Теперь на графике будет показан коэффициент детерминации.

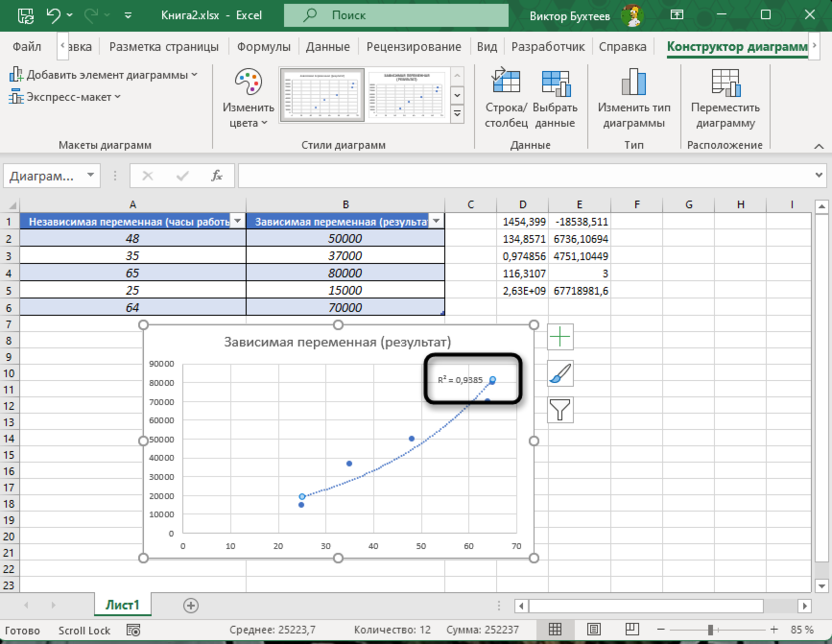
Коэффициент детерминации – это важный показатель для оценки качества линейных моделей. В зависимости от ваших предпочтений и уровня владения Excel вы можете выбрать один из методов: быстрый через линию тренда, комплексный через функцию ЛИНЕЙН или же с использованием корреляции Пирсона.